Çevre yöntemi devre akımının ya da akımlarının çevre ya da çevreler içinde döndüğünü varsayan bir yöntemdir. Buna göre devre akımı üzerinden geçtiği her elemanın üzerinde bir gerilim düşürecektir. Bu gerilimlerin toplamı gerilim kaynağının gerilimine eşittir (şekil-1). Örneğin: R1 direnci üzerine düşen gerilim Ohm yasasına göre I.R1 ; R2 üzerinde düşen gerilim I.R2 olduğu için:
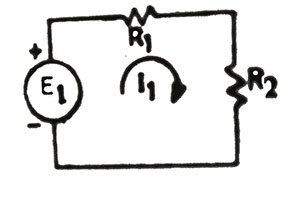
R1.I + R2.I = E ya da (R1+R2).I = E dir. Bu denklem çevre akımı denklemi olarak tanınır.
Çevre içerisinde akım yönünü gösteren okun yönü gerilim kaynağının (+) ucundan çıkacak şekilde alınır. Fakat bu bir kural değildir. İstenilen yön seçilebilir, ancak sonuç (-) çıkıyorsa, yanlış seçim yapıldığının kanıtıdır.
Şekil-2’de iki çevreli bir devre modeli verilmiştir. Burada birinci çevreden geçen akım =I1 ile ; ikinci çevreden geçen akım =I2 ile gösterilmiştir. I1 akımının yönü doğru seçilmiş ve I2 akımının da aynı yönde döndüğü varsayılmıştır. Buna göre ok yönünde başlayarak, I1 akımı sırayla: R1 ve R2 dirençleri üzerinden; I2 akımı ise: R3 , R4 ve R2 dirençleri üzerinden geçecektir. Görüldüğü gibi R2 direncinin üzerinden hem I1 hem de I2 akımı akmaktadır. Aynı direnç üzerinden aynı yönde geçen akımlar toplanır ; aksi yönde geçen akımlar birbirinde çıkarılır. Buna göre birinci çevrenin akım denklemi:
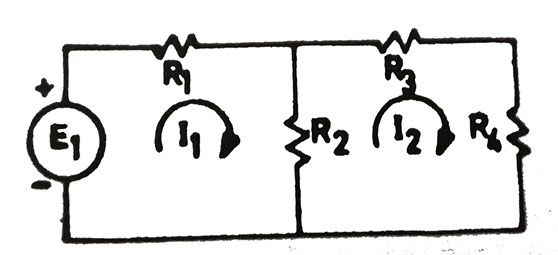
R1.I1 + R2 (I1 – I2) = E1 …dir. (1)
İkinci çevrede gerilim kaynağı olmadığından E2=0 alınır ve
R3.I2 + R4.I2 + R2 (I2-I1) = 0 (2) elde edilir.
Denklemler içinde hangi akımın hangisinden çıkarılacağını saptamak önemlidir. Örneğin I1 akımı denkleminde R2 üzerindeki I2 akımı, I1 akımına ters yönlü olduğundan I1 den I2 çıkarılır. Buna karşın I2 akımı denkleminde R2 üzerindeki I1 akımı I2 akımına zıt yönlüdür, bu nedenle I2 den I1 çıkarılır.
(1) ve (2) de elde edilen denklemler alt alta yazılırsa bunların iki bilinmeyenli iki denklem olduğu anlaşılır ve sonuç bunların ortaklaşa çözümü ile elde edilir.
Çevre miktarı yükselirse, o miktarda denklem çıkarmak gerekmektedir. 3 çevreli bir devre için 3 akım denklemi gerekir.