Kapasitif reaktans

Alternatif akım devresinde kondansatör. Bir doğru gerilim kaynağı bir Kutup çevirici üzerinden 4 µF”lik bir kondansatöre bağlanmıştır. Akım devresine seri olarak alternatif akım ölçen bir ampermetre bulunmaktadır. Bir motorun kollektörüne benzeyen kutup çevirici döndürüldüğünde doğru gerilim, alternatif gerilime dönüştürülür ve devreden alternatif akımın geçtiği görülür. Kutup çevirici daha hızlı döndürüldükçe geçen akımın yükseldiği izlenir.

Kutup çeviricinin döndürülmesiyle, bunun çıkışında doğru gerilim devamlı polarite değiştirir ve bunun sonucu kondansatöre bir alternatif gerilim uygulanmış olur. Bir kondansatöre alternatif gerilim uygulandığında, plakaları değişken bir şekilde pozitif ve negatif yüklenir. Bu farklı yüklenmeler alternatif gerilimin iletken üzerindeki ritmi ile pozitif ve negatife doğru salınır. Bunun sonucu iletkenlerden kondansatöre doğru bir alternatif akım akar. Gerçekte bir kondansatörde alternatif akımın aktığı varsayılır. Bu nedenle buna Bağıl akım ya da İzafi akım denilir.

Alternatif akım devresinde kondansatör geçen akıma bir direnç gibi karşı koyar.

Bu tür bir direnç Kapasitif reaktans (X_C) olarak anılır. Kapasitif reak tansa bazı çevrelerde Kapasitans ya da Kapasitif tepkin direnç de denilmektedir. (Reaktans = Reaktif Rezistans : Tepkin direnç)

Frekans ne kadar yüksek olursa, kapasitans o kadar küçük olur

Yukarıda anılan deneyde 4 µF’lık kondansatör yerine önce 8 µFlik sonra 16 µF”lık kondansatörler konulduğunda devreden geçen akımın yükseldiği görülecektir.

Kapasite ne kadar büyük olursa, kapasitans o kadar küçük olur.

Xc = Kapasitans (Ω)

ω= Açısal frekans (s^-1 veya /rad)

C = Kapasite (F)

X_C = 1 / ( ω . C )

Örnek: 50 Hz lik bir alternatif gerilimde 10 µF lık bir kondansatörün kapasitansını hesaplayınız.

Çözüm:

X_C = 1 / ( ω . C ) = 1 / ( 2 . π . f . C ) = 1/ ( 2 . 3,14 . 50 . 10^-5 ) = 318,5 Ω

Kapasitans bir direnç gibi düşünülürse Ohm yasası burada da uygulanabilir.

Ic = U / Xc

Örnek: Kapasitansi 1600 Ω hesaplanmış bir kondansatöre 50 Hz ve 220 V’luk bir gerilim uygulanmıştır. Devreden geçen akımı bulunuz.

Çözüm: Ic = U / Xc = 220 / 1600 = 0,137 A

Alternatif akım devresinde kondansatör

Paralel devre

Bir çok kondansatörün paralel bağlanması plaka yüzeyinin büyütülmesi gibidir. Bu nedenle C Eşdeğer kapasitesi paralel kapasitelerin tek tek toplamıdır.

Bir çok kondansatörün paralel bağlanmasında eşdeğer kapasite tek tek kapasitelerin toplamına eşittir.

C = C₁ + C₂ + C₃ +…

Örnek: 1000 pF; 0,02 µF ve 5 nF”lık üç kondansatör paralel bağlanırsa eşdeğer kapasite ne olur?

Çözüm:

C = C₁ + C₂ + C₃ = 1000 pF + 20000 pF + 5000 pF = 26000 pF = 0,026 µF

Seri devre

Bir çok kondansatörün seri bağlanmasında Eşdeğer kapasitans seri kapasitansların tek tek toplamına eşittir.

X_C = X_C1 + X_C2 + X_C3 +…

1/ (ωC) = 1/ (ωC₁) + 1/ (ωC₂) + 1/ (ωC₃)

1/C = 1/C₁ + 1/C₂ +1/C₃

Bir çok kondansatörün seri bağlanmasında eşdeğer kapasitenin ters değerliği tek tek kapasite ters değerlerinin toplamına eşittir.

Seri bir devrede eşdeğer kapasite en küçük seri kapasiteden daha küçüktür. Kondansatörlerin seri bağlanması plaka ara mesafelerinin büyütülmesi gibidir. Seri bir devrede bulunan her kondansatörde toplam gerilim bölündüğü için, tüm seri devrenin gerilim dayanımı her bir kondansatörün tek tek gerilim dayanımından büyüktür.

Yalnız iki kondansatörün seri bağlantısında, eşdeğer kapasite :

Örnek: 10 µF ve 2 µF’lık seri bağlanmış iki kondansatörün eşdeğer kapasitesini  bulunuz:

(10 . 2 µF) / ( 10 + 2 µF ) = 1,66 µF

Kondansatörde faz kayması

Şekil : 2’de görüldüğü gibi bir ölçme devresi kurulmuştur. Alternatif akım devresinde kondansatör e seri olarak bir ampermetre ve kondansatöre paralel bağlı bir voltmetre bulunmaktadır. Tüm devre akım devresine bağlanmadan önce bütün ölçü aletleri sıfırı göstermektedir.

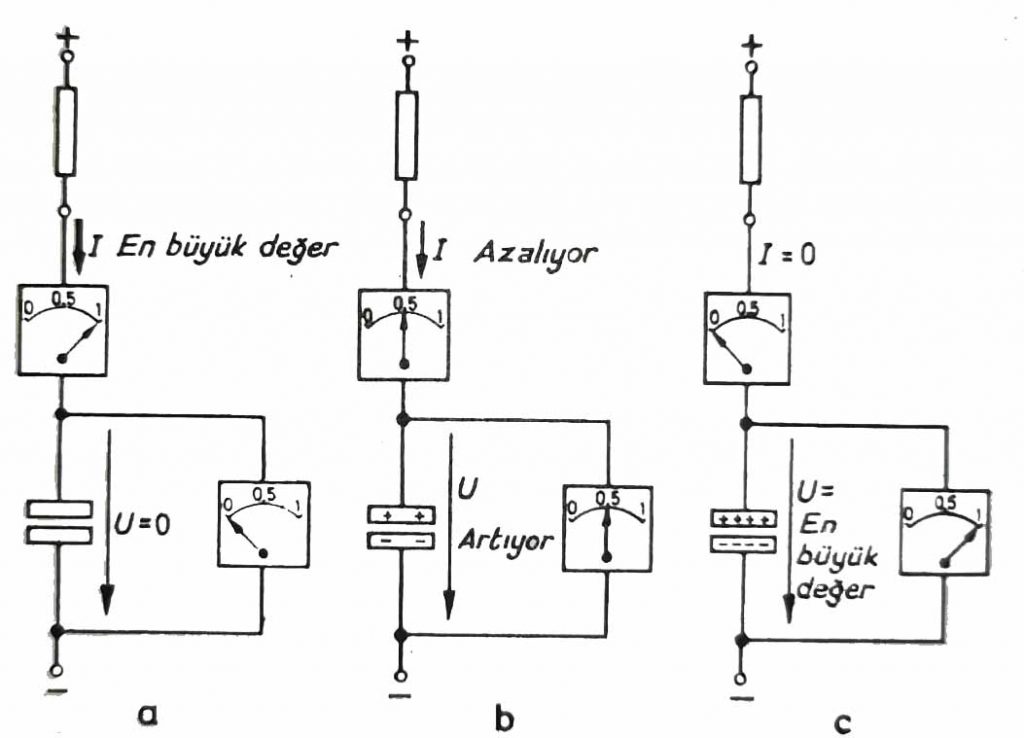
Bu devre örneğin 10 V’luk bir doğru gerilim kaynağına ilk bağlanma anında kondansatör plakaları arasında ölçülen gerilim sıfırdır (Şekil – 2 a). Uygulanan gerilim ile (şarj gerilimi) kondansatör gerilimi arasın da çok büyük bir fark olduğu için, şarjın başlangıcında kondansatöre doğru büyük bir akım akar ve ampermetre en büyük değeri gösterir.

Şarj ilerledikçe kondansatör gerilimi de artmaya başlar. Bunun sonucu şarj gerilimi ile kondansatör gerilimi arasındaki fark azalır ve kondansatöre doğru akan akım düşmeye başlar (şekil – 2 b). Kondansatör tam şarj ettiğinde kondansatör gerilimi ile şarj gerilimi birbirine eşit olur ve şarj akımı sıfıra düşer (şekil – 2 c). Anılan bu evreleri kolaylıkla izleyebilmek için devreye seri halde bir direnç konulmuştur.

Buradan bir kondansatörde, ancak bir şarj akımı ile önceden şarj edilebildiği takdirde, bir gerilimin bulunabileceği anlaşılmaktadır.

Saf kapasitans gösteren bir alternatif akım devresinde akım 1/4 periyot kadar gerilimin önündedir. Bu nedenle gerilim ile akım arasındaki faz farkı açısı 90’dir. (Şekil – 3)

Kondansatörlerde akım gerilimin 90° önünden gider.

Şekil – 1’de görülen devre bir kutup çevirici üzerinde bir doğru gerilim kaynağına (G) bağlıdır. Kutup çevirici döndürüldüğünde, paralel devrede önce kondansatör (C) ayağına bağlı lamba: sonra direnç (R) ayağına bağlı lamba yanacaktır. Buradan bir alternatif akım devresinde bir kondansatörün, bir bobine göre aksi yönde bir faz farkı oluşturduğu anlaşılır.

Alternatif akım devresinde kondansatör kayıpları

Kondansatörlerin hepsinde işletme anında kayıplar ortaya çıkar. Bu nedenle kondansatörler saf kapasitans gösterememektir.

Bu kayıpların bir kısmı, her yalıtkanın bir ölçüde iletken olmasından doğar.

Bir kondansatöre alternatif gerilim uygulandığında dielektrik içindeki moleküler dipoller devamlı döner. Bu nedenle enerjinin bir kısmı ısı halinde yitirilir. Bu özellikten yararlanarak yüksek frekanslarda yakıtkan maddelerin dielektriksel ısıtması yapılır.

Örneğin: Plastik maddelerin yapıştırılması, kerestelerin kurutulması ve kızartma fırınları gibi. (Şekil – 4).

Sargılı kondansatörlerde bağlantı uçları tabakaların başlangıç kısımlarına bağlı olduğu için, şarj akımı şerit şeklindeki sargılar boyunca akmak zorundadır. Bu nedenle bu metal tabakaların da ohmik bir direnci vardır.

Bir kondansatörde anılan bütün bu kayıp türleri Kayıp direnci (R) adı altında toplanabilir. Bütün kayıplar ısı halinde ortaya çıktığından, R kayıp direnci etkin bir dirençtir. Bu etkin direnç bir I_w  Kayıp akımını oluşturur. Bir kondansatörde böyle bir etkin direnç kayıpsız kondansatöre paralel bağlanmış bir direnç halinde düşünülür (Şekil – 5).

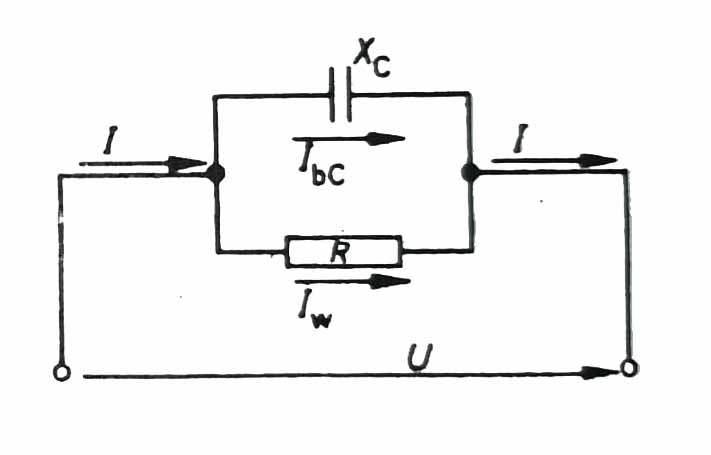
Kayıpları da göz önüne alarak kondansatörler birbirine paralel bağlı kapasitans ve etkin dirençlerle gösterilir.

Dielektrik içindeki kayıplardan dolayı gerilim ile akım arasındaki faz açısı tam 90° olmayıp daima 90° den küçüktür. 90°-φ kadarlık bir fark Kayıp açısı δ (= delta) olarak anılır. (Şekil – 6) iyi kaliteli kondansatörlerde kayıp açısı, bir derecenin 60 – 50 de biri kadardır.

Uygulamada genellikle kayıp açısının tanjantı kullanılır. Kayıp açısının tanjantı Kayıp faktörü olarak anılır.

tanδ = I_w / I_C

Paralel bağlantılı bir devrede kol akımları, üzerinden geçtikleri dirençler ile ters orantılıdır.

I_w / I_bc = X_c / R

Tanδ = 1 / ( ω . C . R )

Kayıp faktörü frekansa bağlı olarak değişir. Ancak bazı hesap işlemlerin de kolaylık getirmesi amacı ile, kondansatörler yalnızca kapasitans halinde kabul edilmekte ve kondansatör içindeki kayıplar ihmal edilebilmektir.

Kondansatörde güç

Saf kapasitif bir yüklenmede alternatif akımın güç eğrisi «u» ve «i»  ani değerlerinin çarpım sonucu elde edilir (şekil – 7). Bu gücün ortalama değeri sıfırdır.

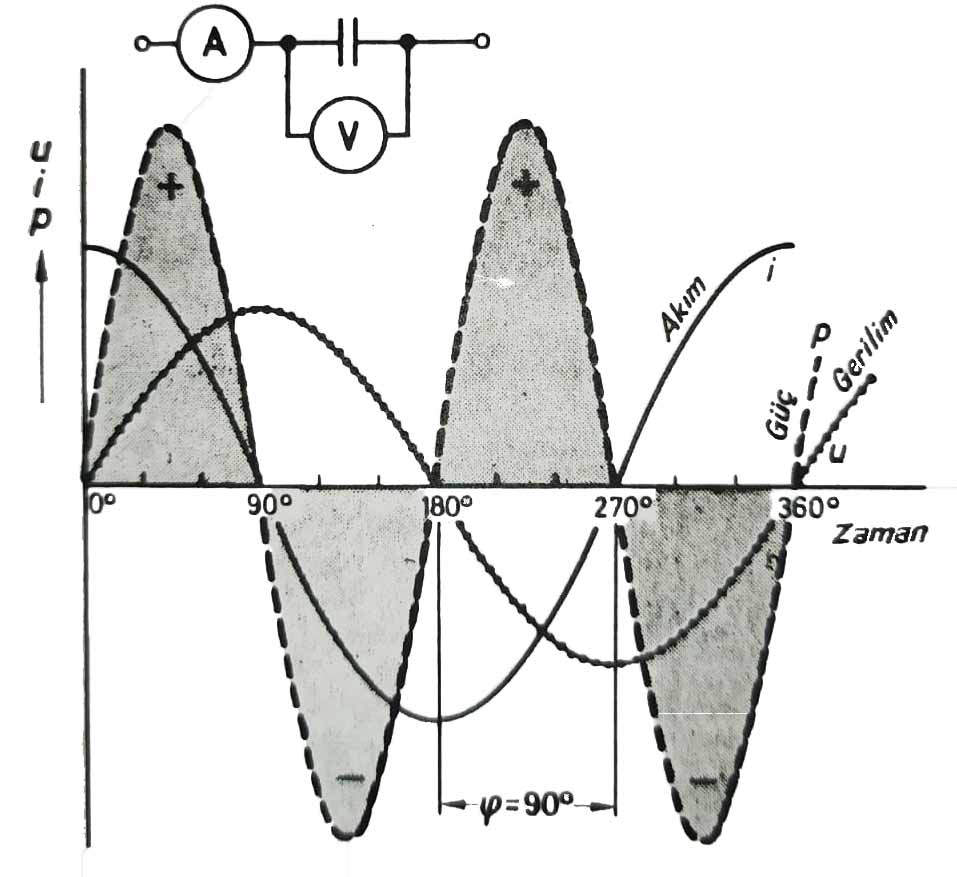
Kayıpsız kondansatörler yalnızca tepkin güç çekerler.

Tepkin güç kondansatör içinde elektrik alanının kurulmasına yarar elektrik alanı yok olduğu zaman bu güç kaynağı geri gönderilir. Bir kondansatördeki enerji kondansatör ile gerilim kaynağı arasında gidip gelerek salınır.

Bundan dolayı kondansatöre giden iletkenlerden tepkin akım geçer.