Bir etkin direnç, örneğin bir elektrik sobası alternatif akım devresine bağlandığında gerilim ve akım aynı fazdadır (Şekil – 1). Gerilim ve akım ani değerlerinin çarpılmasıyla, alternatif akımdaki gücün ani değeri elde edilir. Gerilim ve akım bir etkin direnç üzerinde aynı zamanda negatif ve aynı zamanda pozitif olduğundan, bunların çarpım sonucu elde edilen güç eğrisi daima pozitiftir. Alternatif akımda güç pozitif ise: gücün üreticiden tüketiciye gittiğini belirtir. Gücün frekansı geriliminkine göre iki mislidir. Bu nedenle güç, akım ve gerilimle birlikte ortaklaşa bir vektör diyagramında gösterilemez.

Tepe değeri = u .i olan alternatif akım gücü, alan doldurma işlemi ile (Şekil – 1) eşdeğerli bir doğru akım gücüne yani Etkin güce (Aktif güç) dönüştürülebilir.

Etkin bir dirençte oluşan etkin güç (P), güç tepe değerinin yarısına eşittir.

P = ½ . u . i

= ½ . √2 . U_eff . √2 . I_eff

= U_eff . I_eff

Etkin bir direnç üzerinde oluşan etkin güç, gerilim ve akım etkin değerlerinin çarpımına eşittir.

Alternatif akım gücünün hesaplanmasında daima etkin(effective) değerler kullanılır.

Alternatif Akımda Görünen Güç

Bu kez 50 Hz’lık alternatif gerilime bir endüktör bağlanmıştır. Devrede bir ampermetre, bir voltmetre ve bir wattmetre ölçü aleti olarak bulunmaktadır.

Ampermetrenin ve voltmetrenin gösterdiği değerlerden güç hesaplanıp, walttmetrenin gösterdigi güç ile karşılaştırılırsa, hesaplanmış gücün daha büyük olduğu anlaşılır.

Gerilim ile faz farklı akımın çarpımı Görünen gücü(S) verir. Görünen gücün birimi Voltamper(VA)‘dir.

S = Görünen güç (VA)

U = Gerilim (V)

I= Akım (A)

S=U.I

Buna karşın wattmetreler daima etkin gücü gösterir.

Hem etkin direnci hem de endüktansı olan bir bobinin alternatif akım devresi içindeki güç hesabında, üç farklı güç türü ortaya çıkar, Görünen güç (S) ya da başka bir deyimle Toplam gücün dışında, etkin direnç (R) üzerinde Etkin güç (P) ve endüktans (X) üzerinde endüktif Tepkin güç (Q) oluşur. Tepkin güce Reaktif güç ya da Wattsız güç de denilir. Bunun birimi «VAR» dır (VAR = Volt – Amper-Reaktif).

Gerilim ile akım arasındaki faz farkı 90° ise, pozitif güç alanları, negatif güç alanları ile aynı büyüklüktedir. Bunun sonucu etkin gücün değeri sıfır olur. Negatif gücün anlamı gücün gerilim kaynağına geri verilmesidir. Bir periyot anında enerji iki kez bobinden gerilim kaynağına verilmekte ve tüketici ile üretici arasında enerji gidip gelmektedir. Yani hiç bir iş yapılamaz.

Faz farkı 0° ile 90 arasında ise, akım ve gerilim ani değerlerinin çarpımı, zaman ekseninin üst kısmında daha fazla bir payı bulunan güç eğrisini verir ki, etkin gücün değeri sıfırdan büyük çıkar.Bunun sonucu devrede bir iş yapılmış olur.

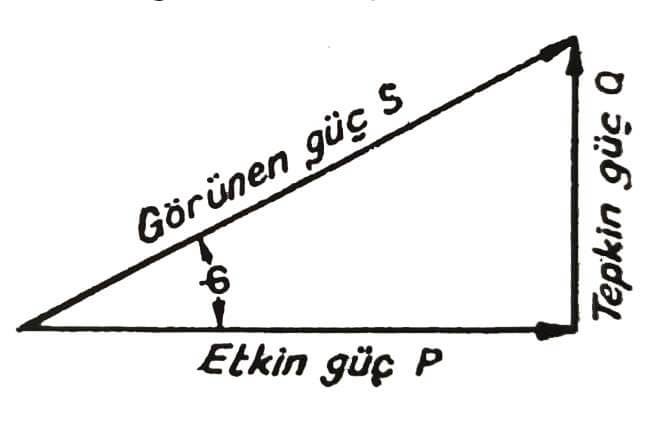
Alternatif Akımda Güç Üçgeni

Güç değerleri de dik açılı üçgen halinde gösterilebilirler. Etkin direnç ile endüktansın oluşturduğu seri bir devrede güç üçgeni gerilim üçgenine eşittir. (S = U . I ; P = U_w . I ; Q = U_bL . I) Çünkü güç formüllerinde kullanılan akım (I) tüm seri – devrede aynıdır. (Şekil – 2)

S² = P² + Q²

S = √(P²+Q²)

Q = √(S²-P²)

P = √(S²-Q²)

S = Görünen güç (VA); Q = Tepkin güç (VAR); P = Etkin güç (W)

Etkin (Aktif) Güç

P ile S arasında ϕ- faz açısı vardır. Faz açısından yararlanarak bu dik üçgende trigonometrik açı fonksiyonları (sinüs, kosinüs) uygulanabilir.

Örneğin : Güç üçgeninde, görünen güç hipotenüs; etkin güç komşu dik kenar ve tepkin güç karşı dik kenardır. Buradan:

kosinüs ϕ = Etkin güç (W) / Görünen güç (VA)

cos ϕ = P / S

P = U . I . cos ϕ

P = S . cos ϕ

Etkin güç : gerilim, akım ve cos ϕ’nin ortaklaşa çarpım sonucudur.

Tepkin (Reaktif) Güç

Güç üçgeninde bu kez sinüs – fonksiyonları ele alınırsa :

Sinüs ϕ =  Tepkin güç (VAR) / Görünen güç (VA)

sin ϕ = Q / S

Q = U.I. sin ϕ

Q = S . sin ϕ

Tepkin güç : gerilim, akım ve sin ϕ’nin ortaklaşa çarpım sonucudur.

Örnek: Bir trafonun sekonder gerilimi 24 V’dur. Sekonder devresine bir ampermetre ve bir yük direnci seri bağlanmıştır, cos ϕ = 0,9 da ampermetrenin gösterdiği değer 2,5 A olduğuna göre : görünen gücü, etkin gücü ve tepkin gücü hesaplayınız.

Çözüm:

S = U . I = 24 . 2,5 = 60 VA

P = S .cos ϕ = 60 . 0,9 = 54 W

Kosinüs tablosu yardımıyla cos ϕ = 0,9 için – faz açısı = 25°50′ bulunur. Bu faz açısı için sinüs tablosundan sin o = 0,4358 olarak saptanır.

Q = S . sin ϕ = 60 . 0,4358 = 26,2 VAR

Alternatif Akımda Güç Faktörü

Etkin gücün, görünen güce oranı güç faktörü olarak tanımlanır.

Güç faktörü = Etkin Güç / Görünen Güç

Sinüzoidal alternatif akımda güç faktörü cos ϕ’nin aynısıdır. Güç faktörü, görünen gücün etkin güce ne oranda dönüştürüldüğü gösteren bir ölçüdür.

Görünen güç = Etkin Güç / Güç faktörü

Etkin güç sabit iken cos ϕ ne kadar küçük olursa, görünen güç ve bununla birlikte akım o kadar büyük olur. Akım değerlerinin büyük tutulması, işletme kuruluş masraflarını artırır. Örneğin : cos ϕ = 0,5 güç faktöründeki bir etkin gücün, cos ϕ = 1 güç faktöründeki etkin güce oranla iki misli büyüklükte bir akım ile taşınması gerektiğinden jeneratör, trafo ve tesisatın buna göre projelendirilmesi zorunlu olmaktadır.

Örnek: Bir fabrika hangarında 220 V/40W lik 200 adet flouresans lamba aydınlatma için kullanılacaktır. Her bir lambanın balast gücü 8 W dır.

a -) cos ϕ = 0,4

b -) cos ϕ = 1 iken ana hattan geçen akımları ayrı ayrı bulunuz.

Çözüm: a -): Her bir lambanın balastı ile birlikte güç çekişi = 48 W’dır.

200 adet lamba için etkin güç = 200.48 = 9600 W = 9,6 kW cos ϕ = 0,4 için görünen güç:

S = P / cos ϕ = 9600 W / 0,4 = 24000 VA = 24 kVA

220 V gerilim altında geçen akım:

I_a = S / U = 2400 / 220 = 109 A

b -) cos ϕ = 1

S = P / cos ϕ = 9600 / 1 = 9600 VA

I_b = S / U = 9600 / 220 = 43,6 A

Buradan cos ϕ = 0,4 iken, cos ϕ = l’e nazaran, en azından 2,5 misli çapta bir ana hat kablosuna gereksinileceği çıkartılabilir.

Tepkin gücün, görünen güce oranı tepkin faktörü ya da reaktif faktör olarak tanımlanır. Sinüzoidal alternatif akımda reaktif faktör sin ϕ ‘ye eşittir.